‍

Introduction

Building machine learning models that perform reliably in production is more difficult than it appears. Even small gaps between training and validation results can signal larger problems in real-world applications.

Addressing these challenges requires careful tuning of model complexity, data quality, and regularization techniques to optimize performance. 

In this article, we will cover:

1. What is overfitting in machine learning
2. Why overfitting occurs: common causes and examples
3. Underfitting vs. overfitting and the bias-variance tradeoff
4. Detecting overfitting: signs and diagnosis
5. How to prevent overfitting: techniques and best practices
6. Overfitting in deep learning: modern insights

Overfitting undermines reliable performance in production. Solving it starts with high-quality, well-curated data.

Lightly allows smarter dataset management to reduce noise, improve data quality, and help models capture the underlying pattern instead of memorizing irrelevant details.

• LightlyOne streamlines dataset curation by automatically removing duplicates, irrelevant samples, and edge cases, resulting in lean, balanced, and realistic data. 
• LightlyTrain works with training workflows to select the most informative data samples, focusing on data that enhances generalization, prevents overfitting, and reduces compute costs.‍
• Lightly AI Training Data Services provide expert support for building high-quality datasets at scale, including tailored labeling strategies for computer vision and LLMs, and curation workflows.

What is Overfitting in Machine Learning?

Overfitting occurs when a machine learning algorithm becomes overly reliant on the training data, resulting in poor generalization. Instead of just capturing the underlying pattern, it also picks up random noise, outliers, and quirks that don’t represent the real world. 

Key signs of an overfit model include: 

• Training–Validation Gap: A sharp drop in training error alongside high validation error shows the model is not generalizing.
• Fitting Noise: Outliers and random fluctuations are treated as predictive patterns.
• Over-Specialization: The model adapts too closely to training data and fails on unseen distributions.

Why is Overfitting a Problem?

A machine learning model is only valuable if it can generalize and make accurate predictions on unseen data. In the case of overfitting, the model cannot pass this test.

It focuses on irrelevant details instead of building a statistical model that captures the true pattern. This leads to poor generalization and an ineffective model.

Why Overfitting Occurs: Common Causes and Examples

Overfitting occurs due to specific factors in the data or model design that lead to poor generalization. These are the primary reasons to be aware of.

• Lack of Training Data: When data is limited, the model will be able to memorize a small sample, which results in high variance and poor generalization.
• Noise or Redundant Features: Datasets usually have noise, errors, or irrelevant data. These signals are valid for an overfit model unless removed through feature selection or preprocessing, which prevents the model from discovering meaningful relationships.
• High Model Complexity: A highly complex model fits the training data too closely by adjusting many parameters. This reduces training error but increases variance and hurts generalization on unseen data..
• Over-Training: Training for too many epochs makes the model memorize noise instead of learning underlying patterns.  It can be prevented with validation, k-fold cross-validation, or early stopping.
• Absence of Regularization: In the absence of constraints, a model will adapt to all the variability of the data. Methods such as L1/L2 penalties, dropout, and feature selection lower the complexity of the model to keep the optimal bias-variance tradeoff.

Real World Example of Overfitting

A recent study showed that deep learning models trained on medical images from one scanner often fail on data from another, even for the same task.

For example, a tumor detection model trained on GE MRI scans identified scanner-specific artifacts. This results in high error rates when tested on Siemens MRI scans. 

Such cases highlight the problem of overfitting, where models capture domain-specific noise instead of the underlying pattern. 

Underfitting vs. Overfitting and the Bias-Variance Tradeoff

Striking the optimal balance between underfitting and machine learning overfitting is the key to creating trustworthy models. This tradeoff defines whether a model can really make predictions on an unseen test dataset.

Underfitting (High Bias)

Underfitting occurs when the model is too simple to accurately explain the underlying pattern in the training data. A high-bias model imposes overly simplistic assumptions, such as linearity, causing it to over-generalize. 

In doing so, it fails to capture nonlinear dependencies and key trends in the data distribution, leading to persistently high error on both training and test sets.

Overfitting (High Variance)

The problem of overfitting may manifest in cases where the complexity of a model exceeds the size of the available data. Variance prevails, and the model is stuck on fluctuations and noise rather than generalizable patterns.

To visualize this, we can consider the classic example of fitting polynomial curves:

Underfitting (Degree 1 Polynomial)

The linear model fails to capture the curvature of the true function. Both training and validation errors remain high, showing high bias and a lack of expressive power. This illustrates an overly underfit model.

Balanced Fit (Degree 4 Polynomial)

The moderate-degree polynomial aligns closely with the underlying pattern without being influenced by noise. Training and validation errors are both low, reflecting a good bias–variance balance. This is where the ML models generalize best to new data.

Overfitting (Polynomial Degree 15)

The polynomial fits almost all training points, including noise. Training error is near zero, but validation error increases, which indicates the model memorizes data rather than generalizing.

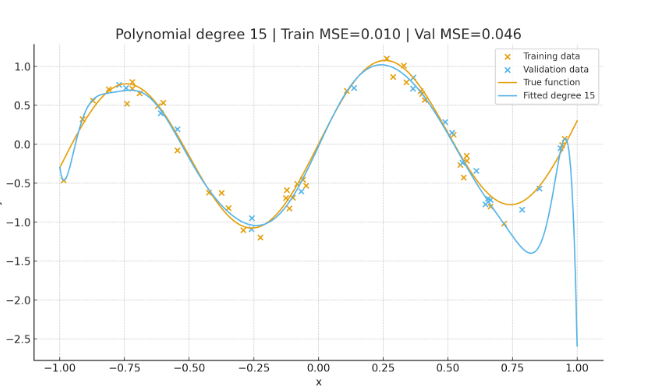
This shows that neither overly simple nor overly complex models generalize well. Reliable performance on new data comes from balancing bias and variance.

Bias-Variance Tradeoff at a Glance

The table below provides a quick comparison of underfitting, overfitting, and the balanced fit in terms of their key characteristics.

‍

Detecting Overfitting: Signs and Diagnosis

Next, we’re going to see how to detect overfitting through practical signs and diagnostic techniques.

• Train vs. Validation Gap: A clear sign of overfitting is a very low training error but a much higher test error, indicating that the model fails to generalize.
• Dedicated Validation Split: Always set aside validation data that the model doesn't see during training. A sharp drop in accuracy on this split compared to training indicates overfitting.
• K-Fold Cross Validation: For smaller datasets, k-fold cross-validation provides a robust check. The model trains on different subsets and validates on hold-out folds, revealing whether it performs consistently or merely memorizes samples.
• Learning Curves: Plotting learning curves for training and validation error helps diagnose overfitting. If training error keeps decreasing while validation error rises, the model captures noise instead of the pattern.
• Model Complexity vs. Data Size: Comparing model complexity to training data size reveals risk. A model with too many parameters relative to data points risks poor performance.
• Prediction Sanity Check: Beyond metrics, manually inspecting predictions can uncover obvious issues. If the model gives unreasonable outputs on simple new data, that’s a practical sign of overfitting.

How to Prevent Overfitting: Techniques and Best Practices

Preventing overfitting is about improving a model’s ability to generalize. These are the most effective strategies:

Train with More Data

The easiest method to avoid overfitting is to increase the training set. As the number of data points increases and covers more diverse situations, the model memorizes less. It adapts better to the underlying pattern, while random noise gets diluted.

Data Augmentation

Data augmentation generates new samples by modifying existing ones in areas such as computer vision. 

Flips, rotations, crops, or adding noise techniques subject the model to varying conditions without needing new labeled data.

Choose a Simpler Model

If a simpler statistical model achieves strong results, prefer it over a highly complex one. 

For example, a linear regression model with polynomial terms may generalize better than a deep network with millions of parameters.

Regularization

Regularization penalizes excessive complexity in training. L2 regularization (ridge) shrinks weights toward smaller values, preventing extreme parameter magnitudes. L1 regularization (lasso) goes further by driving irrelevant weights to zero, effectively performing feature selection. 

Dropout randomly disables neurons during training to reduce co-adaptation and improve generalization in deep learning models.

Ensemble Methods

Combining multiple models helps reduce variance. Bagging trains models on bootstrapped data, while boosting improves weak learners sequentially. Both stabilize predictions and prevent poor generalization.

Active Learning

In areas where the data is obtainable through iteration, active learning focuses on labeling the most uncertain or informative samples. This makes every new data point valuable and minimizes the possibility of overfitting.

Cross-Validation for Model Tuning 

Using k-fold cross-validation during hyperparameter tuning ensures the chosen configuration generalizes across equally sized subsets of data. This avoids selecting a model that only works well on a single train–test split.

Feature Selection

Too many irrelevant features increase model complexity and variance. Feature selection filters out inputs with little predictive power, helping the model focus on meaningful relationships.

Early Stopping

When training error keeps decreasing but validation data error starts to rise, it means the model is memorizing noisy data instead of learning patterns. Early stopping halts training at the point of best generalization, striking a balance between bias and variance.

Overfitting in Deep Learning: Modern Insights (Double Descent)

Traditionally, increasing model complexity reduces error. But once overfitting sets in, test error rises, reflecting the bias–variance tradeoff in classical ML.

Double Descent Phenomenon

In modern deep learning, error can decrease, rise, then decrease as complexity grows. When models become highly over-parameterized, they can sometimes generalize better than smaller ones.

Why It Happens

Once a model fits the training data perfectly, additional flexibility enables it to identify smoother and more stable functions. 

Implicit regularizers, such as stochastic gradient descent (SGD), drive solutions to patterns that reflect the underlying structure rather than noise memorization.

Implications for Practice

• Large, highly parameterized models can sometimes generalize better than mid-sized models.
• The double descent effect means the risk of poor generalization is highest in the intermediate complexity regime.
• Techniques like regularization, early stopping, and cross-validation remain essential safeguards against overfitting.

How Does Lightly Prevent Overfitting Through Data Selection?

Lightly reduces overfitting by applying embedding-based sampling strategies that ensure datasets stay diverse and representative. Its diversity strategy enforces a minimum distance between embeddings, removing duplicates and near-identical samples that inflate variance. 

The typicality strategy prioritizes high-density regions in the embedding space. This ensures the model learns from the most representative examples rather than outliers or noise. 

These approaches produce compact, info-rich datasets, reducing noise memorization and improving generalization. This data-first method tackles overfitting at its source.

Conclusion

Overfitting restricts the model’s ability to generalize from training data to new data. Techniques such as regularization, early stopping, data augmentation, and cross-validation help mitigate this risk. Vigilance is still required, even with modern effects like double descent. 

The goal remains the same, which is to capture the underlying pattern, not the noise, since relying on noisy data often means the model performs poorly on unseen examples.