A Brief Guide to Cross-Entropy Loss
Table of contents
Cross-entropy loss measures how well a model’s predicted probabilities match the actual class labels. Widely used in classification tasks, it penalizes confident wrong predictions and provides informative gradients that improve training and convergence.
Quick answers to common questions about Cross-Entropy Loss:

- What is cross-entropy loss?
Cross-entropy loss compares the probability distribution predicted by a model with the actual class labels. It is the common loss in classification tasks, as it directly evaluates the certainty of model predictions.
Cross-entropy determines whether the predicted class was correct, and penalizes the model based on its confidence. When the correct class is assigned a high probability, the loss is low. When the incorrect class is assigned a high probability, the loss is high.
Cross-entropy can be used with training models that output class probabilities. This includes the softmax function in multi-class classification and the sigmoid function in binary classification.
- Why is cross-entropy used?
Cross-entropy helps models assign higher probabilities to the correct classes and provides well-calibrated probability estimates instead of a binary decision. Cross-entropy loss is logarithmic, which causes a large gradient on incorrect predictions. This implies that the loss will penalize large deviations of the correct label more than small ones.
For example, predicting a probability of 0.2 when the true label is 1 results in a much greater error than predicting 0.8. These informative and sharp gradients enable the model to make significant parameter updates, particularly during the initial stages of training.
Cross-entropy produces a convex objective function for the weights of the last layer, particularly when using logistic or softmax output layers. This convexity makes it more stable and reliable to optimize.
Compared to other losses like mean squared error, cross-entropy produces more informative gradients during training. This leads to faster convergence and better generalization.
- What is binary cross-entropy?
Binary cross-entropy is a variant of cross-entropy loss that is used to address binary classification tasks, which require the output to be either 0 or 1.
Rather than comparing a full probability distribution across multiple classes, it compares a single predicted probability (of the positive class) with the true binary label. This renders it appropriate in models that have a sigmoid output layer.
This loss function is defined as:
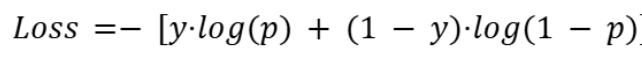
where:
- y is the true label (0 or 1),
- p is the predicted probability for the positive class.
The function heavily penalizes incorrect predictions that are made with confidence. For instance:
- If the true label is 1 and the model predicts 0.9, it indicates low loss (~0.105),
- If it predicts 0.1, it indicates a high loss (~2.302).
It is also known as log loss or logistic loss in logistic regression and binary neural classifiers.
- What is the formula for cross-entropy?
The overall cross-entropy expression is used to quantify the difference between two probability distributions, the actual distribution P and the estimated distribution Q, as follows:
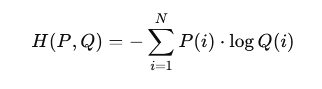
In classification tasks:
- P(i) is the ground truth distribution, often one-hot encoded (i.e., 1 for the correct class, 0 elsewhere),
- Q(i) is the model’s predicted probability for class i,
- N is the number of classes.
For most practical cases (with one-hot labels), this simplifies to:
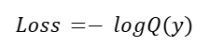
Q(y) is the probability of the correct class being predicted. This implies that the model will be penalized depending on the amount of probability it assigns to the actual class.
This is a direct formulation for multi-class classification problems, which is usually coupled with softmax activation functions in the output layer.
A Brief Guide to Cross-Entropy Loss
Developing precise deep-learning classifiers requires loss functions that provide stable, informative gradients over high-dimensional outputs. Cross-entropy loss scales gradients with prediction error, prevents late-training collapse, and supports higher learning rates. Such reliability enhances convergence and increases generalization to a variety of tasks.
This guide will cover the cross-entropy loss formulation, key variants, and its behavior in model training.
In this guide, we will cover:
- What is cross-entropy loss
- Types of cross-entropy loss functions
- Cross-entropy loss in machine learning and deep learning
- Cross-entropy loss behavior with predicted probabilities
Choosing the right loss function is key, but the quality of the data feeding into your model is just as important for achieving stable, reliable training. At Lightly, we help you get the most out of your model training with:
- LightlyOne: Select the most representative and impactful samples so your model learns from the right examples.
- LightlyTrain: Pretrain and fine-tune models to take full advantage of curated datasets for faster convergence and better generalization.
Together, they complement techniques like cross-entropy loss to deliver stronger, more accurate models.

What is Cross-Entropy Loss?
Cross-entropy loss is a measure of the difference between two probability distributions, the ground truth distribution P and the predicted distribution Q of the model.
Under classification, P is usually a one-hot encoded vector (all mass on the correct class), and Q is the softmax or sigmoid output of the model.
The cross-entropy loss formula is:
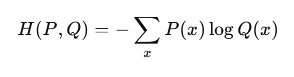
This formulation is based on information theory, where cross-entropy measures the average number of bits required to code samples of P with a code optimized to Q. When Q equals P, the value represents the entropy of P. If Q differs from P, the cost increases.
Entropy vs. Cross Entropy
While entropy measures the randomness of a true distribution, cross-entropy evaluates the discrepancy between the predicted and true distributions. Their connection is fundamental to the comprehension of model performance in classification.
Cross-entropy can be viewed mathematically as the sum of the entropy of the true distribution and the KL divergence between the true and predicted distributions. That is, it not only reflects the uncertainty of the data but also discourages deviations from correct predictions.
Let’s have a look at the comparison table:
Intuition (Surprise and “Bits”)
In information theory, rare events convey more information than common ones. For example, a coin landing on its edge, which is rare, tells you more than if it lands on heads, which is common.
Entropy captures this idea by quantifying the average uncertainty in a distribution. Cross-entropy loss extends this further by calculating the number of bits required to represent true outcomes given the distribution predicted by the model.
Training a classifier with cross-entropy loss involves adjusting the distribution Q predicted by the model to represent the true labels with fewer bits. This means the model needs to make correct predictions and assign probabilities that match the true distribution.
Cross-Entropy as a Distance
Although cross-entropy is not a valid distance measure (it is not symmetric), it indicates the direction of distribution mismatch.
Specifically, it measures the inadequacy of a predicted distribution Q to the true one P. The cross-entropy loss increases as Q shifts probability mass toward areas where P is mainly concentrated.
Example
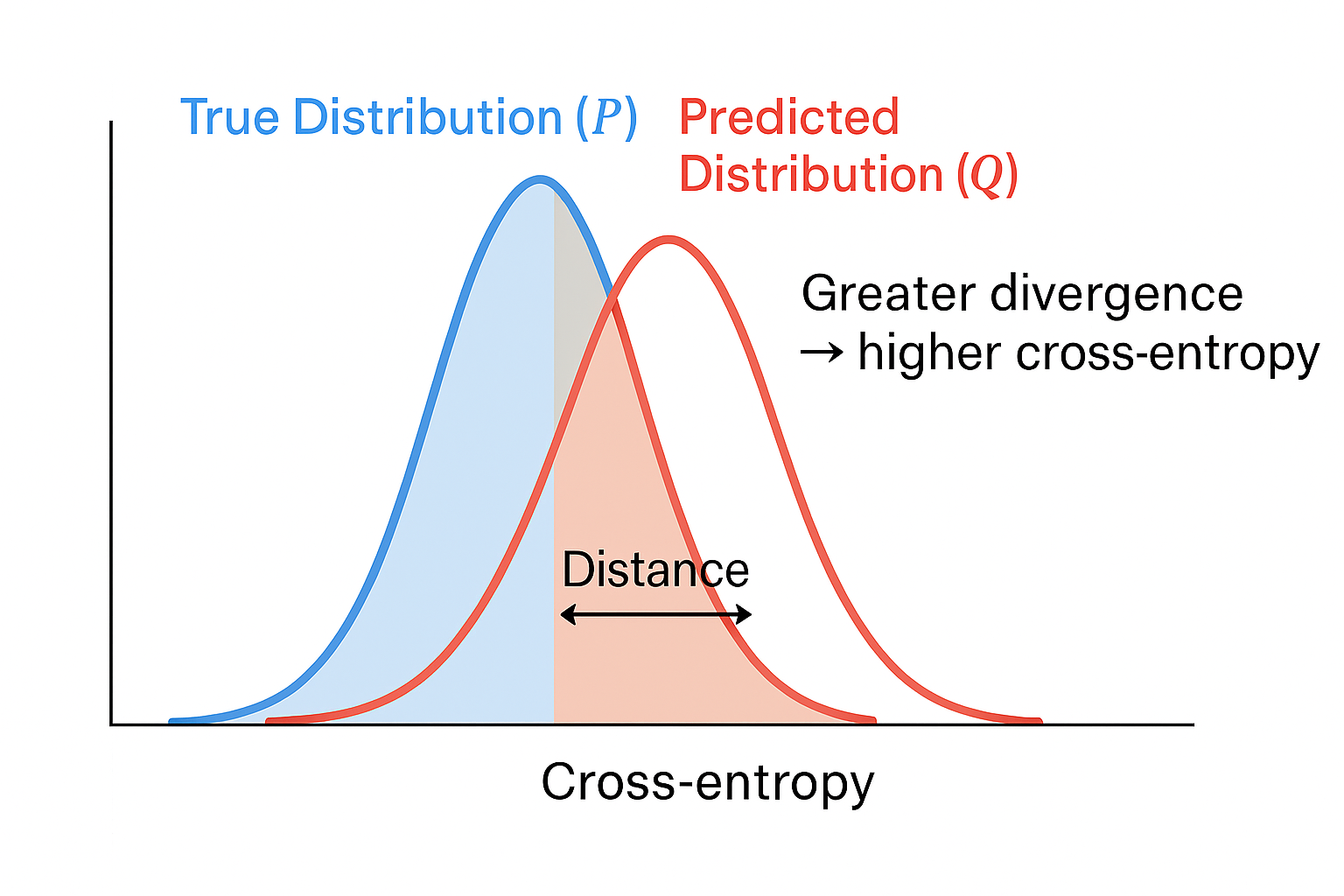
Suppose the true distribution is:
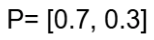
Now compare three different model predictions Q:
In this case, the second prediction is identical to P, and the resulting loss is the entropy of the real distribution. The remaining branches expand, resulting in an increased average cost of encoding the actual outcome with a mismatched prediction.
Pro Tip: For better feature separation in low-label scenarios, try contrastive learning. It trains the model to group similar inputs closer and separate different ones, improving representation quality even with limited labeled data.
Types of Cross-Entropy Loss Functions
Various classification tasks require customized cross-entropy loss formulations that are more representative of label structure and computing requirements.
The most prominent types address binary classification, multi-class classification, and multi-label classification scenarios.
Choosing the Right Loss Function for Classification
Cross-entropy is a core component of classification models. Its performance depends on the loss function, output layer, labeling scheme, and model architecture. Let’s explore its two variants:
- Binary Cross-Entropy (BCE): Binary cross-entropy loss is applied in binary classification or multi-label classification, where each output is a separate binary decision. It uses a sigmoid activation function on the output layer, which converts logits to independent predicted probabilities in the range of [0, 1]. Unlike softmax, sigmoid doesn’t assume classes are exclusive.
- Categorical Cross-Entropy (CCE): Categorical cross-entropy is used in multi-class classification, where the input belongs to exactly one class. It applies a softmax activation to transform logits into a normalized probability distribution over all classes. This makes the model produce only one correct instance of a class.
Pro Tip: Strong embeddings boost classification model robustness. Mapping similar items close in embedding space makes your model more efficient and robust, and reduces confusion in class indices.
Binary Cross-Entropy (Log Loss)
Also known as log loss, binary cross-entropy calculates the penalty for predicting a probability that diverges from the true distribution in binary outcomes.
Use Case
It's used in binary classification (two classes) and multi-label classification (independent binary decisions per label). Common applications include:
- Recognition of spam (spam or not spam)
- Medical diagnosis (whether a disease is present, or not)
- Multi-label tagging (e.g., multiple labels on an image)
Output Activation
Requires a sigmoid activation function on the output unit. This converts logits to independent probabilities between the [0,1] range.
Loss Computation
For a single binary output:
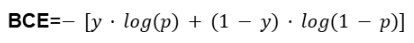
Where:
- y∈{0,1} is the true label
- p∈[0,1] is the predicted probability after sigmoid
In multi-label cases, it is calculated separately for each label and then averaged across outputs.
Behavior
- Non‑Exclusive Predictions: The classes are treated separately (e.g., with sigmoid activation), so the predicted probabilities do not need to add up to 1. This makes BCE suitable for multi-label classification.
- Class Imbalance Weighted: Loss for each class can be weighted, often by the inverse of class frequency.
- Multi‑Label Support: The loss sums independent binary cross-entropy losses per class, with inputs labeled with any set of active labels, not just one winner.
- Error Sensitivity in Prediction: When the predicted probability is significantly different from the actual label (e.g., predicting 0.1 when the true label is 1), the loss is high. When the prediction is similar to the actual value (e.g., 0.9 vs 1), the loss is small. This steep gradient assists in correcting significant errors within a short time.
Example
CheXNet, a neural network (121‑layer DenseNet), was trained on more than 100,000 chest X‑rays to detect 14 diseases. It used weighted binary cross-entropy loss to address the issue of class imbalance, with rare diseases getting larger weights.
The performance of the resulting model had an F1 score of 0.435, which was better than the F1 of the average radiologist of 0.387.
Categorical Cross-entropy
Use Case
Categorical cross-entropy is the standard loss function for the multi-class classification tasks in which each input has a single, pre-defined label among N mutually exclusive classes. For example, in digit recognition (e.g., MNIST), each image is labeled as a single digit from 0 to 9.
It is the default option when you have a single correct class and want to fit a probability distribution over all possible classes.
The typical applications are:
- Image classification (e.g., CIFAR-10, ImageNet)
- Sentiment analysis (positive/neutral/negative)
- Language modeling (predicting the next word using a vocabulary)
Output Activation
The CE model requires a softmax activation function for its output layer. Softmax is a function that transforms raw logits into a probability distribution with a sum of 1. This makes the model outputs mutually exclusive and appropriate for single-label classification activities.
Loss Computation
The categorical cross-entropy loss is computed as:
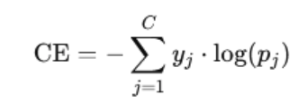
Where:
- C - total number of classes
- y_j - one-hot encoded true label vector
- p_j - predicted probability for class j
Behavior
- Inter‑Class Competition: Drives competition between classes. The higher the probability for one class, the lower the probabilities for others.
- Confidence Maximization: The model maximizes confidence in the correct class while minimizing it for others.
- High‑Confidence Error Sensitivity: Sensitive to inaccurate high-confidence predictions, which is useful for training well-calibrated classifiers.
- Class Imbalance Mitigation: In imbalanced classes, weighting or sampling may be required to prevent bias toward frequent classes.
Example
Sentiment classification of movie reviews is a complicated process because people express their views in subtle and varied ways. A recent study used a BERT-based neural network with a bi-directional LSTM to incorporate forward and backward context.
The training of this classification model involves categorical cross-entropy to facilitate confident prediction of the true label among various sentiment classes. The parameters of the model are optimized to minimize the entropy loss in all the predictions.
In binary sentiment classification (positive vs. negative), the model achieved 97.7% accuracy. While in fine-grained multi-class classification (e.g., 5 classes of sentiment), it achieves 59.5% accuracy.
Binary vs Categorical Cross-Entropy
The following table highlights key differences between binary cross-entropy (BCE) and categorical cross-entropy (CCE).
Cross-Entropy vs. Mean Squared Error (MSE)
A common point of confusion in classification tasks is whether to use cross-entropy loss or mean squared error. Here’s how they compare across key dimensions.
Cross-Entropy Loss vs. Hinge Loss
To understand when to use cross-entropy loss or hinge loss, especially in classification tasks, here’s a technical comparison of the key differences:
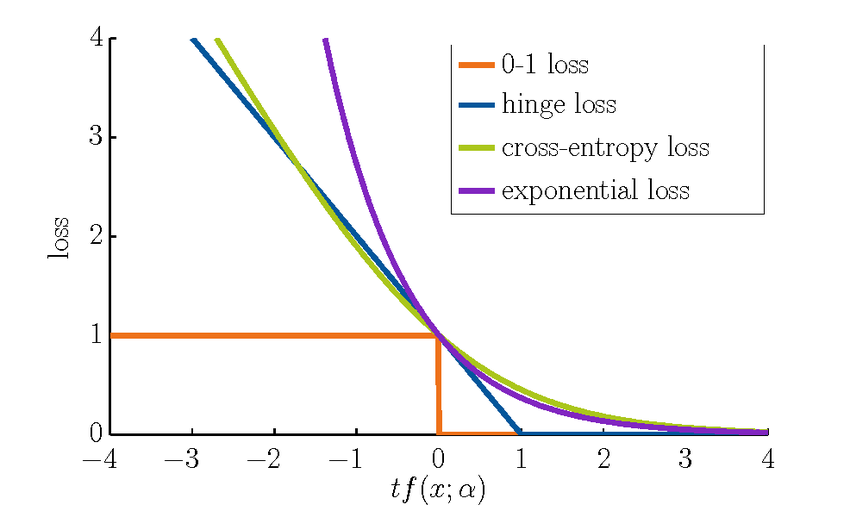
Cross-Entropy Loss vs. Negative Log-Likelihood (NLL)
Cross-entropy and negative log likelihood loss are usually the same in supervised classification tasks. NLL is the negative log-probability of the correct class of the model. Cross-entropy is a generalization of this concept, the expected log-loss with respect to a true probability distribution (typically one-hot).
The implementation of cross-entropy loss is usually numerically safer due to the fusion of log-softmax and NLL steps. The separate computation of softmax and log can be less stable when using NLL.
Both maximize the log-likelihood of the correct label, which strengthens the same statistical principle. But in end-to-end pipelines, cross-entropy is more commonly used because it has implicit preprocessing.
When Might You Not Use Cross-Entropy?
Cross-entropy loss isn't suitable for regression with continuous targets. Instead, use MSE or MAE. It is sensitive to noisy labels or outliers, as incorrect confident predictions are heavily penalized, risking unstable training.
Additionally, in these situations, more robust regression techniques or other loss functions can be appropriate. These reduce the impact of overconfident mistakes and prevent training collapse.
In the case of noisy target labels or significant class imbalance, focal loss is more suitable. Focal loss alters the cross-entropy by reducing the weight of easy-to-classify examples and increasing the loss of hard-to-classify examples.
This prompts the model to prioritize complex samples, enhancing performance in skewed or noisy data without compromising the essence of cross-entropy.
Loss Functions Comparison Table
The following table provides a technical comparison of common loss functions used in classification tasks, highlighting their strengths, weaknesses, and ideal use cases:
Cross-Entropy Loss in Machine Learning and Deep Learning
The classification problem in machine learning is generally framed as the task of aligning probability distributions through cross-entropy loss. The model is designed to predict a distribution over classes, with training focused on minimizing the distance to the true distribution.
In logistic regression, the cross‑entropy loss arises directly from maximizing the Bernoulli likelihood. In logistic regression, we model the probability of the positive class:
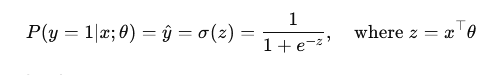
For binary labels y∈{0,1}, the Bernoulli likelihood of a single prediction is:
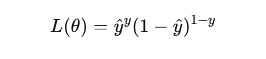
Taking the negative log-likelihood to get the loss:
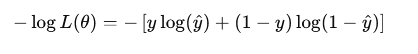
So, the binary cross-entropy loss is:
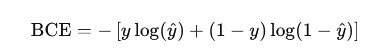
This principle extends to deep learning, where neural networks parameterize the likelihood function, and optimization is performed via stochastic gradient descent or its variants.
Compared to losses like MSE, cross-entropy provides more precise gradients and faster convergence. It also offers better-calibrated probability estimates, which improve training dynamics.
Pro Tip: You don’t always need labels to pretrain powerful models. Self-supervised learning lets the model learn useful features on its own, which can later be fine-tuned with cross-entropy loss.
Cross Entropy in Pytorch
In PyTorch, cross-entropy loss works directly on raw logits to measure the prediction error at the class level and does not require explicit probability normalization.
It combines log_softmax and negative log-likelihood internally, offering both computationally efficient and numerically stable. These features make it a commonly used loss function in classification tasks.
Implementation and Use Cases in Neural Networks
Cross-entropy loss is common in training neural networks to classify. Now, let us see how it is applied in common cases and use examples.
Framework Implementations
PyTorch loss functions used in classification tasks are closely tied to the design of the output layer. Let’s look at the implementation of multi-class classification:
This is used for single-label, multi-class problems, where each input belongs to exactly one of CCC classes.
- Input (logits): shape [batch_size,num_classes][ \text{batch\_size}, \text{num\_classes} ][batch_size,num_classes], raw scores (no softmax applied)
- Target: shape [batch_size][ \text{batch\_size} ][batch_size], class indices (integers)
- Internally: combines LogSoftmax + NLLLoss
Now, let’s look at the implementation using PyTorch:
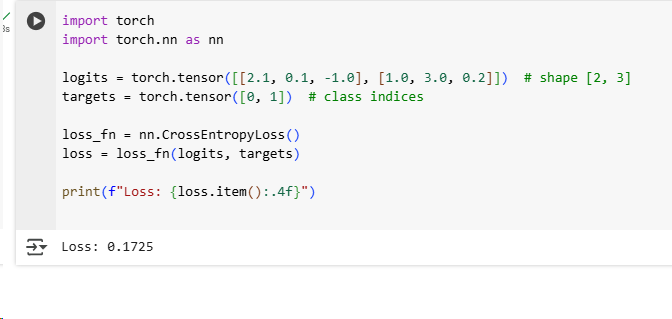
This result (Loss: 0.1725) indicates that the model is making correct predictions with reasonably high confidence, though it is not perfectly accurate.
Example Use Cases
With the fundamentals in place, let's see how it can be applied across a variety of real-world use cases.
Behavior During Training
Cross-entropy loss generates high gradients on confidently wrong predictions, which allows the model to quickly rectify its errors. Gradients decrease as the model's predictions approach the true labels, which results in stable convergence.
This process helps the model concentrate its probabilities on the correct class, which improves both training efficiency and generalization.
Integration with Gradient Descent
Cross-entropy loss generates steep, non-zero gradients even in the case of incorrect classes. This makes it highly suitable to train classification models using gradient descent. As a result, the model converges faster and learns more effectively, especially in deep learning systems.
Cross-entropy, unlike MSE, does not suffer from the problem of gradient saturation, and the signal propagates strongly through backpropagation. This behavior allows neural networks to better match predicted probabilities to true labels, which speeds up learning and boosts accuracy.
The diagram below highlights the loss and gradient behavior during binary classification:
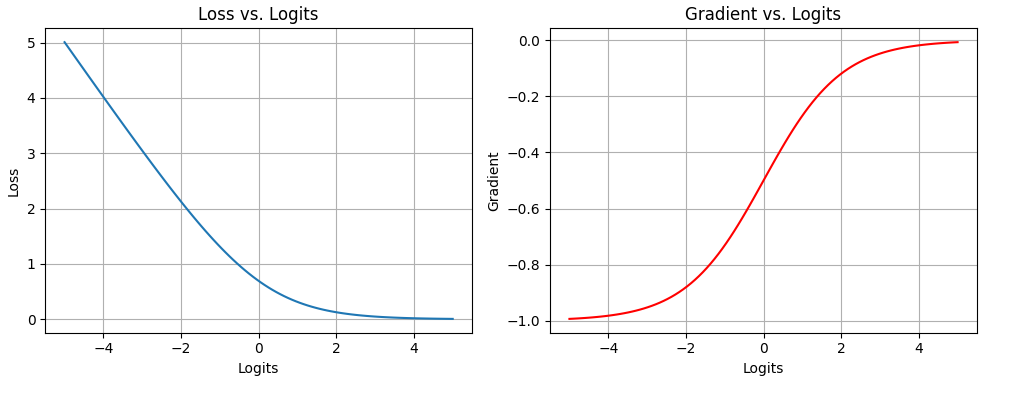
This diagram shows the behaviour of cross-entropy loss and its derivative during binary classification training. The loss punishes incorrect high-confidence predictions (left plot), encouraging the model to be more confident in correct predictions.
Meanwhile, the gradient (right plot) has the largest absolute value when the model is most incorrect, which guarantees successful updates at the initial stages of training. Both loss and gradient fade out as predictions get better, stabilizing learning.
Real-World Example
In this example, we train a simple convolutional neural network on the CIFAR-10 dataset using PyTorch with cross-entropy loss.
Code
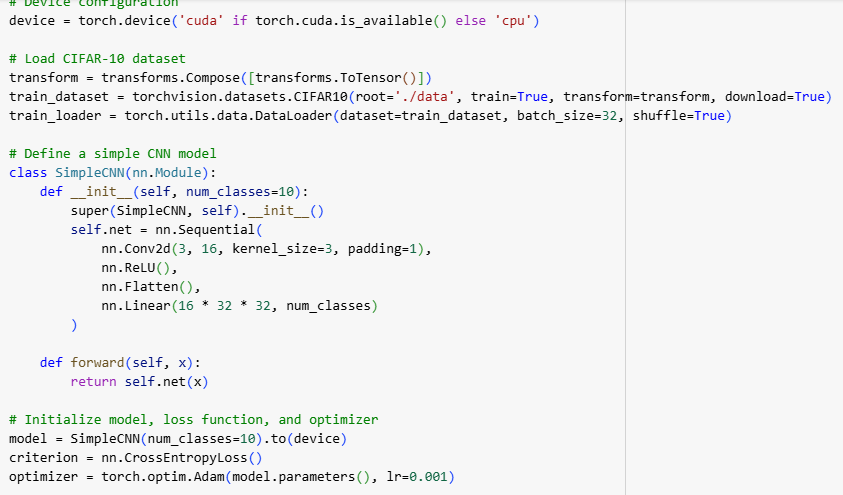
Result
During early training, model predictions are often inaccurate. As training progresses and weights adjust, the loss steadily decreases as the model learns to align its predictions with the correct classes. Here is the loss curve during learning:
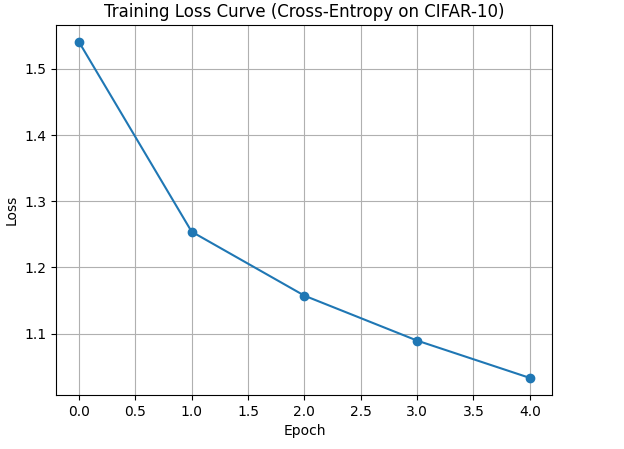
The steadily decreasing loss across epochs indicates effective learning and model convergence.
Cross-Entropy Loss Behavior with Predicted Probabilities
Cross-entropy loss offers a smooth, differentiable signal indicating how well predicted probabilities match true labels. It rapidly decreases as the correct class probability increases, rewarding confident, accurate predictions.
Binary Case Behavior
In binary classification, where the model's probability is close to the true label (0 or 1), the loss will be close to zero. But if the model assigns a high estimated probability to the wrong class, the penalty grows steeply.
This asymmetry helps the model overcome overconfidence during the initial stages of training data.
Multi-Class Behavior
When a high probability is incorrectly assigned to the wrong class in multi-class scenarios, the loss increases. Cross-entropy encourages the model to adjust probabilities, ensuring that the final layer’s confidence is focused on the correct target.
- Correct class vs Incorrect classes: The loss function is minimized when the model parameters drive the network to assign complete confidence to the correct class. On the other hand, when the probability is placed on the wrong classes (i.e., over-belief), the loss is higher.
- Gradient Perspective: Due to its sharp slope around high-confidence errors, cross-entropy ensures that any incorrect prediction will induce significant updates through gradient descent. This property avoids vanishing gradients and supports solid early optimization.
- Confidence Penalty and Saturation: False positives are costly because training with cross-entropy penalizes overconfidence in wrong categories more than underconfidence in correct ones. Plateaus and saturation occur when predicted values near certainty (0 or 1). This results in smaller updates that prevent late-stage training instability.
- Edge Cases: Cross-entropy exhibits extreme values on the edges of the predicted probabilities. Minimum loss occurs when the label and the predicted class are equal with a probability of 1. Maximum loss is unbounded when the estimated probability of the correct class is near zero, due to the logarithmic penalty on confident mistakes.
Training Interpretation
Cross-entropy is used as a training signal, and points out where the model is uncertain or confidently wrong. This feedback process refines the model parameters, which allows for performance optimization even with noisy or complicated data.
Cross-Entropy and Model Uncertainty
Softmax produces uncertain, nearly uniform probabilities, which increases loss even if the top guess is correct. This indicates the model's reluctance and highlights the need to define decision boundaries better.
Cross-Entropy and KL Divergence
The minimization of cross-entropy with one-hot labels is mathematically identical to minimizing KL divergence. From an information theory perspective, this involves reducing the number of additional bits of information needed to define the actual labels using the estimated distribution.
How Lightly AI Improves Cross-Entropy Loss Training
Cross-entropy performance is closely related to data quality, representation learning, and training efficiency.
This is where Lightly AI comes in, not to replace cross-entropy, but to improve the conditions in which it is optimized. Let’s have a look:
LightlyTrain
LightlyTrain is a self-supervised pretraining method that does not require labeled data to train CNNs and Vision Transformers. It uses contrastive learning techniques like SimCLR and DINOv2 to create effective feature extractors from raw images.
When these pretrained backbones are later fine-tuned with cross-entropy loss on downstream classification tasks, the models tend to optimize better. This approach becomes especially useful when you’re dealing with small or imbalanced labeled datasets, because it helps the training process stay more consistent.
LightlyEdge
LightlyEdge is a real-time edge SDK to capture high-value training data. It assists in implementing smarter data collection strategies in distributed or production environments.
For cross-entropy trained models:
- Training data is aligned with real-world distributions
- Duplicate low-value samples are removed, reducing the risk of overfitting
- Loss values are prioritized for rare or edge-case inputs that drive high loss values
LightlyEdge ensures that your classification model is being trained on the right data, where cross-entropy loss is most important.
Conclusion
Cross-entropy loss optimizes classification tasks by minimizing the difference between predicted and true label distributions. It works well with softmax activations, preserving distributional semantics, unlike regression losses.
This results in more stable convergence, better label sparsity, and refined confidence calibration. As a result, cross-entropy remains the default loss function for deep learning models.

Stay ahead in computer vision
Get exclusive insights, tips, and updates from the Lightly.ai team.




.png)
.png)
.png)


